Газовые законы

Основы молекулярно-кинетической теории.

 

 

 

 

 

 

 

 

Введение:

 

 

 

 

 

 

Давление газа есть не что иное, как суммарное воздействие молекул, находящихся в замкнутом объеме.

Закон Бойля—Мариотта. Между давлением газа и объемом, который он занимает, имеется определенная связь. Закон, описывающий эту связь, открыли независимо один от другого английский химик Р. Бойль и французский физик Э. Мариотт. Поэтому этот закон называют законом Бойля—Мариотта. Согласно этому закону давления одного и того же количества газа при неизменной температуре обратно пропорциональны объемам, занимаемым этим количеством газа. Например, если некоторое количество газа сжимается до половины своего первоначального объема, то давление в газе увеличивается в 2 раза, и наоборот, если объем, который занимает количество газа увеличится в 2 раза, то давление уменьшается в 2 раза. Математически этот закон записывается уравнением

P₁W₁=pW,                                                           (19)

где р₁ и W₁— начальные давления и объем; р и W —давление и объем газа при любых условиях.

Этот закон объясним с позиций кинетической теории газа. Переместим поршень влево, уменьшая тем самым объем, занимаемый газом. При этом время, затрачиваемое молекулами на возвращение к поршню, уменьшится, а число ударов молекул о поршень увеличится. Следовательно, возрастет и суммарное действие молекул на поршень, что приведет к повышению давления.

Интересную трактовку понятия «давление газа» можно получить, если подсчитать работу ∆А, которую надо затратить для перемещения поршня на расстояние ∆x (рис. 13). Известно, что работа — это произведение силы на перемещение. Согласно выражению (18)

Тогда

∆A=F∆x=pS∆x. Так как S∆x=∆W — изменение объема, то

                                            ∆A = p∆W.        (20)

Из выражения (20) имеем

p = ∆A/∆W.          (21)

Таким образом, давление газа можно определить как энергию единицы объема газа.

Температура. Кинетическая теория газов связывает одно из физических свойств — температуру с движением молекул. Если два газа имеют одинаковую температуру, то средние кинетические энергии молекул этих газов равны. Средняя кинетическая энергия молекул — это свойство температуры. Если два газа имеют различную температуру, то средняя кинетическая энергия молекул больше у газа, температура которого выше. Такая модель дает возможность объяснить тот факт, что при сжатии температура газа возрастает, а при расширении уменьшается. Очевидно, что скорость частиц газа, ударяющихся о движущийся им навстречу поршень, увеличивается после отталкивания от него. Следовательно, средняя кинетическая энергия молекул га за, а значит и температура, возрастают.

Для измерения температуры пользуются абсолютной термодинамической шкалой температур Кельвина (К) или стоградусной шкалой температур Цельсия (°С). Связь между этими двумя шкалами определяется выражением

T=273,16+t        (22)

 

где Т — температура тела по абсолютной термодинамической шкале Кельвина; t — температура тела по международной сто градусной шкале Цельсия.

В стоградусной международной шкале при нормальном атмосферном давлении р= 100 кПа=10⁵ Па за 0°С принимается температура тающего льда, а за 100°С — температура кипения воды.

В абсолютной термодинамической шкале температур Кельвина за нуль принято состояние тела, при котором тепловое движение молекул практически отсутствует. Из выражения (22) видно, что абсолютный нуль соответствует температуре

t= — 273,16°С.

Абсолютная термодинамическая шкала Кельвина и между народная стоградусная шкала Цельсия имеют один масштаб, т. е. приращение температуры на 1⁰С равно приращению температуры на 1 К, что дает возможность достаточно просто определять абсолютную температуру по формуле (22).

Закон Гей-Люссака. Французский ученый Гей-Люсcак обнаружил, что повышение температуры на 1°С влечет за собой увеличение объема газа на 1/273,16 того объема, который этот газ занимает при 0°С, при условии, что давление газа при изменении температуры остается постоянным. Математически этот закон выражается уравнением

                         W=W₀(1+at),       (23)

где Wo — объем   газа   при   температуре   t=0°С;   a =1/273,16 град^-1 — коэффициент расширения.

Удельным объемом газа V₀ называется отношение объема газа к его массе m=pW. Тогда

V₀=W/m=l/p.         (24)

Исходя из полученного выражения можно записать

V_oρ—1       (25)

т. е. произведение удельного объема   на плотность равно единице.

Пользуясь выражением (24), закон Бойля—Мариотта пере пишем в виде

pVo=p₁V₀₁                                                            (26)

где Vo₁ — удельный объем газа при давлении р₁. Закон Гей-Люссака

                         Vo=V₀₁(1+at).                                                           (27)

Уравнение (27) можно   преобразовать.   Согласно   выражению (22) имеем

                                  1 + at=1+a (T-273,16)=aT.

Тогда

Vo=V_o1aT.                                                          (28)

Используя выражения (26) и (28), можно получить уравнение, связывающее давление р, удельный объем V₀ и температуру Т. Так как уравнение (26) соответствует расширению газа при постоянном давлении, оно справедливо для обоих состояний газа. Умножив обе части уравнения (28) на равные давления, соответствующие этим состояниям, получим

pV₀=P₁V_o1aT.                                  (29)

Так как р1 и Voi — параметры состояния газа при температу­ре 0°С, то при T₀=273,16° имеем

а= 1/273,16= 1/T₀.

Выражение

pVo/T = PiVo1/To                                                   (30)

называют уравнением Клапейрона или уравнением состояния идеальных газов.

Реальные газы ведут себя несколько иначе, однако при обычных плотностях состояние реальных газов хорошо описывается уравнением (30). Отклонения заметны только при значительном сжатии газа и особенно при пониженной температуре газа, когда происходит его сжижение.

Для 1 моля газа можно подсчитать значение poVo/To.

Для всех газов оно является константой и называется универсальной газовой постоянной R. Для рассматриваемого случая

R=8,314.10з Дж/(кмоль-К).

Для 1 киломоля газа уравнение состояния имеет вид

pV₀RT.                                                             (31)

Согласно выражению (25) уравнение состояния газа можно привести к виду

P/p=RT.                                                          (32)

 

Идеальный газ. Первый закон термодинамики.

 

Термодинамические процессы

Термодинамика - это наука, изучающая свойства систем на основе законов превращения энергии. Как правило, в задачах термодинамики определяют связь между механической, внут­ренней и тепловой энергиями. Изменение одного из этих видов энергии влечет за собой соответствующие изменения других.

Системы, которые изучают законы изменения энергии называются термодинамическими. Рассмотрим такую термодинамическую систему, в которой изменения энергии протекают в газовой среде. Как уже указывалось, состояние газа определяется следующими параметрами: давлением р, температурой Т и удельным объемом Vo. Совокупность названных основных параметров выражается уравнениями (31) и (32).

Допустим, что газ, находящийся между стенками цилиндра и поршнем, взаимодействует с внешней средой (пусть под действием внешних сил поршень сжимает газ). В результате этого взаимодействия изменяются параметры газа и его внутренняя энергия (при сжатии температура газа возросла).

В другом случае, если к газу подводят теплоту извне, например, газ нагревают через стенки цилиндра, то газ расширяется, и, следовательно, совершает работу по перемещению поршня. При этом внешняя среда теряет теплоту. Таким образом, изменение энергии внешней среды, вызванное потерей теплоты и полученной работой, должно быть по абсолютной величине равно изменению внутренней энергии газа.

Аналогичную связь между теплотой, работой и внутренней энергией газа характеризует первый закон термодинамики, который можно записать в виде

        ∆Q=∆U + ∆A,        (33)

где ∆Q — теплота, которой обменивается масса газа с окружающей средой; ∆U — изменение внутренней энергии массы газа; ∆A — механическая работа, затрачиваемая на сжатие или расширение массы газа.

Из уравнения (33) следует, что подведенная к газу теплота изменяет его внутреннюю энергию и обуславливает совершение им механической работы.

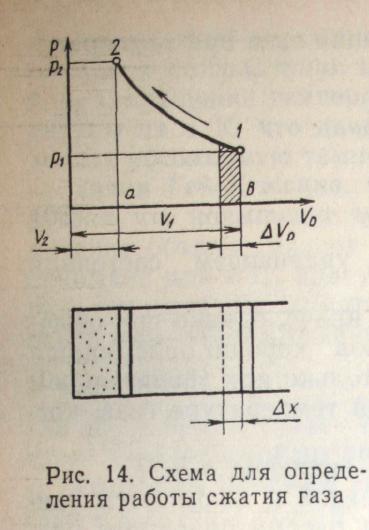
В поршневом компрессоре затрачивается механическая работа на сжатие газа. Пусть процесс перемещения поршня из положения 1 в положение 2 соответствует кривой 1-2 в координатах Р— Vо (рис. 14). Чтобы выразить работу сжатия через основные параметры состояния, обеспечим некоторое перемещение поршня на ∆х. Определим работу как произведение силы на перемещение. Поршень совершает движение против сил давления, равных pS (S — площадь поршня). Тогда работа

∆A=pS∆x.

Так как произведение S∆x является изменением объема газа в цилиндре, то

∆A=р∆V.    (34) 

Разделим обе части выражения (34) на массу газа ∆m, находящегося в объеме ∆V.  Тогда ∆А1=∆A/ ∆m -удельная   работа сжатия, ∆V=∆ V/∆m — удельный объем газа. 

Окончательно   ∆А₁=р∆V₀.   (35)

Выражение (35) показывает, что работу сжатия в поршне­вом компрессоре можно измерить площадью под кривой процес­са (заштрихованная областъ), а для конечного процесса, про­ходящего от точки 1 до точки 2 — площадью фигуры а-Ь-1-2.

Таким образом, системой координат р—Vo очень удобно пользоваться для определения работы, совершаемой при сжатии или расширении газа. Эта система координат удобна также тем, что она позволяет получить представление об «алгебраическом знаке» процесса. Если происходит процесс расширения газа (∆Vo>0), to работа совершается газом. Если происходит сжа­тие газа (∆Vo<0), то работа совершается окружающей средой. 

Поэтому первый закон термодинамики в случаях, когда р = const можно представить в виде

∆q = ∆u-\-p∆V₀,                                                         (36)

где ∆q — удельная теплота, ∆q<7=∆Q/∆m; ∆u — изменение удельной внутренней энергии ∆u=∆U/∆m.

Из курса физики известно, что изменение теплоты

∆q=с_р∆T                                                             (37)

где с_р — удельная теплоемкость газа при постоянном давлении,

Дж/(кг*К).

Изменение внутренней энергии

∆u=c_v∆T,                                                              (38)

где Сv — удельная теплоемкость газа при постоянном   объеме,

Дж/(кг*К).

При постоянном давлении изменение температуры газа ∆T зависит от изменения его объема ∆Vo. Поэтому

                 p∆V₀=R∆T.                                                             (39)

Подставим выражения  (37) —(39) в уравнение (36). Тогда

_Cp∆T=c_v∆T+R∆T.

Из последнего выражения можно определить связь между удельной теплоемкостью газа при постоянном давлении и удельной теплоемкостью газа при постоянном объеме, т. е.

                                                        c_p-c_v=R.            (40)

Для упрощения расчетов многих термодинамических процес­сов, протекающих в тепловых машинах, используется функция, называемая энтальпией:

H=u + pV₀.  

Физический смысл энтальпии состоит в том, что при любых процессах, происходящих в газе при постоянном давлении, изменение энтальпии ∆Н пропорционально изменению температуры ∆T и равно количеству теплоты, поглощенной или отданной газом, т. е.

∆T=∆q=с_р∆T                                                            (41)

Подобно тому, как работа, затрачиваемая на сжатие газа, выражается площадью р-Vо-диаграммы, можно таким же образом определить количество теплоты, получаемое при различных изменениях состояния газа. Эта площадь определяется в другой системе координат.

Немецкий физик Рудольф Клаузиус ввел понятие энтропии, обозначаемой символом S, изменение которой определяет коли­чество подведенной или отведенной теплоты ∆q, т. е.

∆q = T∆S.                                                           (42)

Для определения физического смысла энтропии произведем некоторые преобразования уравнения (36), описывающего первый закон термодинамики. Из выражения (38) получаем

∆q=c_v∆T+ p∆V₀.

Из уравнения состояния газа (31) следует

T = pVo/R.

Используя выражение (42) и приведенное выше равенство, получаем выражение изменения энтальпии,

∆S=∆q/T=c_v ∆T/T + R ∆V₀ / V₀      (43)

Конечное изменение энтропии S₂—S₁ при изменении состоя­ния газа от p₁, V_01, T₁ до р2, V₀₂, T₂ определяется уравнением, доказательство которого приводится в более сложных курсах термодинамики:  S₂-S₁=Cv ln T2/T1 + R ln V02/V01                                                                               (44)

  Таким образом, изменение энтропии не зависит от протекания термодинамического процесса. Как видно из выражения (44), энтропия является однозначной функцией состояния га за. Это дает возможность выбирать энтропию в качестве одного из независимых переменных в диаграммах, в которых определяется количество   теплоты,   сообщенной телу при сжатии или расширении газа.

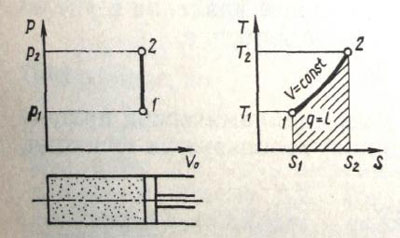
Рис. 15. Зависимость работы от теплоты при изохорном процессе.

 Проиллюстрируем использование p—V₀ и T-S-диаграмм в различных термодинамических процессах.

Изохорный процесс. При нагревании или охлаждении газа в цилиндре при неподвижном поршне (герметично закрытый со­суд) имеет место термодинамический процесс, происходящий при постоянном объеме. Этот процесс называется изохорным, т. е.

V₀=const;   ∆V₀=0.                                                     (45)

Уравнение изохорного процесса можно получить, если в уравнении состояния идеального газа (31) принять условие, опи­сываемое уравнением (45), т. е.

 р/Т=const.                                                       (46)

 Следовательно, при изохорном процессе при повышении температуры давление газа возрастает.

Рассмотрим изохорный процесс в координатах р—V₀ и Т—S (рис. 15). Пусть до нагрева газ (точка 1) находился в состоянии, характеризуемом давлением р₁, температурой T₁ и энтропией S₁. После подвода теплоты q газ (точка 2) имеет давление p₂>p₁ и температуру T₂>T₁. При изохорном процессе V₀=const, поэтому в р—Vo-диаграмме точки 1 и 2 находятся на одной вер тикали, соответствующей условию Vo=const.

Выражение (46) показывает, что поскольку ∆V₀=0, газ ра боту расширения не совершает, т. е. ∆A₁=0 и вся теплота нагрева расходуется на увеличение внутренней энергии. Если газ, обладая внутренней энергией, совершил работу, то на р—V₀ диаграмме она характеризуется площадью 1-2-р₁-р₂. Так как ∆q = ∆u, то для конечного процесса, протекающего от точки 1 до точки 2, получаем

S₂-S₁=C_v 1n T2/T1                                                 (47)

 Очевидно, что энтропия газа с повышением температуры возрастает. Точка 2 на Т—S-диаграмме лежит выше и правее точки 1. Таким образом, площадь фигуры S₁-1-2-S₂ определяет количество подведенной к газу теплоты. Одновременно при изо­хорном процессе эта же площадь характеризует прирост внут­ренней энергии.

Изобарный процесс. Термодинамический процесс, протекаю­щий в цилиндре, поршень которого перемещается без трения таким образом, что после подвода теплоты давление в цилиндре остается постоянным, называется изобарным.

Для такого процесса

p=const;  ∆p=0.                                                           (48)

 Уравнение изобарного про­цесса может быть получено из уравнения состояния {выраже­ние (31) или (44)]:

V₀/T= const.        (49)

Как видно из выражения (49), объем газа увеличивается при изобарном процессе с повыше­нием температуры.

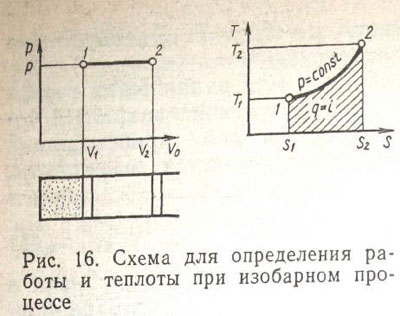
Рассмотрим изобарный про­цесс в р—Vо- и Т—S-диаграммах (рис. 16). Пусть газ занимал объем V₁ при давлении р₁, имел температуру Т₁ и энтропию S₁. После подвода теплоты ∆q при выполнении" условия, характеризующегося выражением (48), газ занимает объем V₂>V₁ при Т₂>Т₁. Так как ∆р=0, то выражение (44) показывает, что газ совершил работу расши­рения, которая для конечного процесса, проходящего от точки 1 до точки 2, определится площадью фигуры V₁-1-2-V₂ согласно уравнению (44), т. е.

∆q = ∆H.                                                           (50)

Таким образом, вся теплота при нагреве расходуется на изменение энтальпии газа. Используя выражения (50) и (44), получаем

∆S = c_p(∆T/T).

Для конечного процесса, протекающего от точки 1 до точки 2, имеем 

Lq=ku-\-kA_v           (51)

Это выражение показывает, что при нагреве газа при изо­барном процессе энтальпия его возрастает и точка 2 на Т—S-диаграмме располагается выше и правее точки 1. Количество теплоты, переданное рабочему телу, определится площадью фигуры S\-l-2-S₂.

Так как при изобарном процессе подведенная теплота расхо­дуется на изменение внутренней энергии газа и совершение работы расширения, то для количественного определения рас­пределения теплоты можно воспользоваться первым законом термодинамики. Тогда

Lq=ku-\-kA_v

Разделив обе части равенства на ∆q, получим 

∆A₁/∆q=1 - ∆u/∆q .  (52)

 Используя выражения (44) и (50), можно переписать выражение (52) в виде

 ∆A₁/∆q = 1 - C_V /C_P       (53)

Здесь с_р, c_v — удельные теплоемкости газа соответственно при постоянном давлении и объеме.

Отношение удельных теплоемкостей k = c_p/c_v называют пока­зателем адиабаты.

Таким образом,

∆A₁/∆q = 1 - 1/k . 

Для двухатомных газов k= 1,405. Следует отметить, что при изобарном процессе 29% подведенной к рабочему телу теплоты расходуется на совершение работы, а 7% — на изменение внут­ренней энергии.

Изотермный процесс. Известно, что процессы сжатия и рас­ширения газа сопровождаются изменением всех параметров его состояния (объема, давления и температуры). При сжатии, нап­ример, выделяется теплота. Однако, если сжатие газа произво­дить медленно и давать возможность выделившейся теплоте через стенки рассеяться в окружающую среду, то справедлив закон Бойля—Мариотта, так как сжатие происходит при посто­янной температуре. Термодинамный процесс, который проте­кает при постоянной температуре, называется изотермный. В этом случае

T = const;   ∆T=0.      (54)

Уравнение изотермного процесса, полученное из уравнения состояния, имеет вид

pV₀=const.

Следовательно, при изотермном процессе сжатия или расширения уменьшение объема приводит к повышению давления, и
наоборот.

Из уравнения (44) видно,   что   при   изотермном   процессе

∆H=∆u=0, т. е.
∆q = ∆A₁          (55)

Таким образом, теплота целиком расходуется на работу расширения газа (А₁).

На рис. 17 изображен изотермный процесс в р-Vо- и T-S-координатах. Если осуществлять сжатие газа, при котором постоянно отводится теплота, то работа А₁ на р-V-диаграмме соответствует площади р₁-1-2-S₂, а теплота, отводимая от цилин­дра,—площади S_1-1-2-S₂, — на T—S-диаграмме.

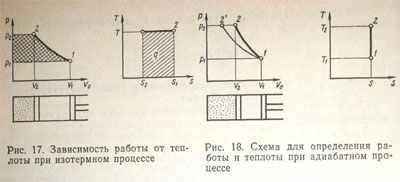
Наоборот, если теплоту подавать через стенки цилиндра и газ изотермически расширять от V₁ до V₂ то совершаемая работа на р—V₀-диаграмме определится площадью V₂-2-1-V₁. Площадь Т—S-диаграммы будет той же самой.

Адиабатный процесс. Рассмотрим случай, когда термодина­мический процесс сжатия или расширения газа протекает так быстро или стенки цилиндра так хорошо изолированы от влия­ния внешней среды, что теплота не поглощается или выделяется наружу. Такой термодинамический процесс называется адиабат­ным, т. е. без обмена теплотой с внешней средой. При адиабат­ном процессе

                               ∆q=0 q=const.     (56)

В этом случае связь между давлением и удельным объемом газа определяется уравнением адиабаты

                               pV^ko = const.      (57) 

Показатель адиабаты для двухатомных газов (азот, водород, воздух, кислород, окись углерода) k = 1,40÷1,41; для трех- и многоатомных газов (аммиак, ацетилен, метан, пропан углекис­лый газ) k =1,1 ÷1,33

Исходя из услсвия, соответствующего выражению (56), из выражения (44) следует

∆H =V0∆p=∆A₁;

∆u =p∆V₀=∆A₁; 

∆S =0.                     (58)

Это означает, что на р—Vo-диаграмме (рис. 18) работа сжатия, определяемая площадью фигуры p₁-1-2-p₂, равна изменению энтальпии, а работа расширения газа, определяемая площадью фигуры V₂-2-1-V₁ , обусловлена изменением внутренней энергии.