Давление
Торетические основы сжатия воздуха и различных газов.
Если на тело действуют внешние силы, то в теле возникают силы реакции, направленные в сторону, противоположную действию сил, что обусловлено межмолекулярными связями. Выделим из общего объема небольшой замкнутый объем жидкости или газа. В этом случае силы реакции располагаются на поверхности выделенного объема. Произвольно действующую по отношению к поверхности силу реакции разложим на две составляющие (касательную и нормальную). Касательная составляющая, обусловленная вязкостью, действует вдоль поверхности элемента жидкости и проявляется только во время движения жидкости или газа. Нормальная составляющая силы реакции существует как в процессе движения, так и в покое.
Рассмотрим жидкостную систему, находящуюся в равновесии. Пусть имеется сосуд, содержащий объем жидкости или газа. Расположим внутри объема этой жидкости произвольным образом плоскость ЛВ, которая разделит массу жидкости на две массы I и II. Если отбросить массу II, то для того, чтобы равновесие остального объема не нарушалось, необходимо в каждой точке поверхности ЛВ ввести силы, уравновешивающие воздействие массы II на оставшуюся часть жидкости.
Предположим, что эти силы направлены произвольно к поверхности АВ (точное направление их неизвестно). Считаем, что поверхность состоит из маленьких площадок размером AS. На элементарную площадку действует произвольно направленная сила ∆R. Разложим эту силу на две составляющие (нормальную ∆F и касательную ∆T к поверхности). Если в жидкости действует касательная составляющая силы, то она не может находиться в покое, так как жидкость обладает текучестью, т. е. отсутствием сопротивления сдвигающим нагрузкам. Это означает, что если жидкость находится в покое, то в ней отсутствуют касательные составляющие силы реакции. Таким образом, внутренние силы реакции, возникающие в жидкости, находящейся в состоянии покоя, должны быть перпендикулярны любой точке поверхности внутри жидкости и направлены внутрь объема. Если площадь ∆S достаточно мала, то отношение нормально действующей силы реакции ∆F к площади ∆S называют нормальным напряжением сжатия в точке. В гидравлике нормаль ные напряжения сжатия, возникающие в жидкости или газе, называют давлением и обозначают символом р. Итак, давление
p=∆F/∆S. (6)
Как видно из выражения (6), давление — размерная величина, измеряемая в Па (1 Па=1 Н/м2).
Из формулы (6) видно, что одна и та же сила может вызвать различное давление. Например, если одно и то же усилие распределить на большую площадь, то давление, вызываемое этим
Схема для определения давления в жидкости, находящейся в равновесии под действием только сил тяжести, усилием, окажется меньше. Лыжник, движущийся по снежному полю, не проваливается в снег, так как его вес распределен на большую поверхность лыж, что вызывает меньшее давление на снег по сравнению с давлением, возникающим от человека без лыж.
Следовательно, мы выяснили, что в жидкости или газе (покоящемся или движущемся) всегда есть давление. Определим, везде ли оно одинаково в жидкости. Рассмотрим равновесие жидкости, находящейся в относительном покое в гравитационном поле. Примером тому является жидкость, налитая в какой-либо сосуд (рис. 7).
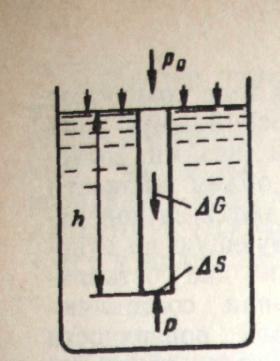
Выделим в жидкости некоторый вертикальный призматический объем, в котором площадь его основания достаточно мала и равна ∆S.
Чем меньше эта площадь, тем с большим основанием можно утверждать, что давление на нее в любой точке одинаково. Тогда, согласно выражению (6), на площадку ∆S действует сила F=p∆S.
Допустим, что площадка ∆S находится на глубине h, а на свободную поверхность жидкости действует давление р0. Так как весь объем жидкости находится в относительном покое (по отношению к стенкам сосуда жидкость неподвижна), то для составления уравнения равновесия необходимо суммировать все силы, действующие на выделенный объем жидкости, и приравнять их нулю. Поскольку мы предположили существование только гравитационного поля, то на этот объем жидкости действует ее вес AG, равный объему W—h∆S, умноженному на удельный вес жидкости y» и направленный вертикально вниз, т. е.
∆G = yh∆S. (7)
С другой стороны, на поверхность выделенного жидкого элемента объема действует сила давления, направленная по нормали к поверхности. Для определения равновесия жидкости в поле гравитационных сил спроектируем все силы, действующие на выделенный объем, на вектор силы тяжести. Тогда проекция силы давления, действующей на боковую поверхность этого объема, равна нулю, и из поверхностных сил останутся только те, которые действуют на торцовые поверхности. Если за положительное направление принять направление гравитационной силы ∆G, то суммарная сила давления ∆F, действующая на торцовые поверхности,
∆F=р0∆S - p ∆S. (8)
Итак, уравнение равновесия для выделенного элемента объема
∆G + ∆F=0.
Подставим
вместо ∆G и ∆F их значения из выражений (7)
и (8). Тогда
yh∆S+p0∆S-p∆S=0.
Сократив в последнем уравнении все члены на ∆S, получим выражение, определяющее давление в любой точке покоящейся жидкости:
p = po+yh. (9)
Полученное выражение называют основным уравнением гидростатики.
Из уравнения (9) видно, что давление в любой точке покоящейся жидкости можно разложить на давление р0, приходящееся на свободную поверхность, и давление yh, зависящее от глубины расположения этой точки. Следует отметить, что частицы жидкости, находящиеся на одинаковой глубине h, испытывают одинаковое давление.
Таким образом, горизонтальная плоскость, расположенная в однородной жидкости, находящейся в равновесии под действием сил тяжести, является плоскостью равного давления.
Давление р называется абсолютным давлением в точке, pо называется внешним, а произведение yh— весовым давлением.
Распространены случаи, когда внешнее давление равно атмосферному. Тогда весовое давление yh называют избыточным. Абсолютное давление всегда положительно. Избыточное давление может быть положительным (если оно больше атмосферно го) или отрицательным (если оно меньше атмосферного).
Проведем плоскость О—О (рис. 8), где абсолютное давление равно нулю, и плоскость А—А, где абсолютное давление равно атмосферному. Эти две плоскости являются плоскостями отсчета. От плоскости О—О вычисляют атмосферное давление, а от плоскости А— А — избыточное давление. Пусть в точке b давление превышает атмосферное. Тогда избыточное давление в точке b
Рвизб=уh, (10)
а абсолютное давление в точке b
pвабс = pатм + yh, (11)
Допустим, что в точке с давление меньше атмосферного. Избыточное давление в точке с pcизб =yh; pcвак= yh;
абсолютное давление p сабс = p атм-yh. (12)
Приборы, предназначенные для измерения давления, показывают значение избыточного давления.
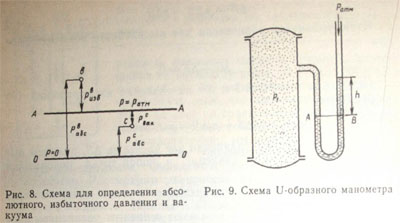
Пусть в сосуде находится газ под некоторым избыточным давлением. Если подсоединить к этому сосуду U-образную трубку, то жидкость, находящаяся в трубке, поднимется на высоту h. Высота h соответствует избыточному давлению р1 в сосуде. Так как система находится в равновесии в поле гравитационных сил, то любая горизонтальная плоскость, проведенная в однородной среде, является плоскостью равного давления. Если плоскость АВ провести в U-образной трубке, то давление в этой плоско сти будет одинаковое. Тогда Ра=Рв.
Избыточное давление в точке В
Рв=уh. (13)
Избыточное давление в точке А, если пренебречь массой газа, pA = p1
Согласно выражению (13) имеем
P1=yh. (14)
Откуда h=p1/y, т. е. высота поднятия жидкости в U-образной трубке действительно соответствует избыточному давлению газа в сосуде. Такая высота называется пьезометрической.
Основной частью жидкостных манометров являются различные U-образные трубки. Для того чтобы не отсчитывать уровень жидкости в двух сечениях трубки, одно из ее колен выполняют в виде широкого сосуда (рис. 10). Если пренебречь колебанием уровня жидкости в сосуде, то высота подъема жидкости в трубке будет соответствовать разности давлений:
p2 — Pi=yh-
Жидкостный пьезометр обычно используют для измерения атмосферного давления (рис. 10).
Если из сосуда A, соединенного с сосудом В, в который налита жидкость плотностью y, откачать воздух, то в соединительной трубке за счет давления, создаваемого наружным воздухом, жидкость поднимется на высоту h. Давление в точке 1, расположенной на глубине h,
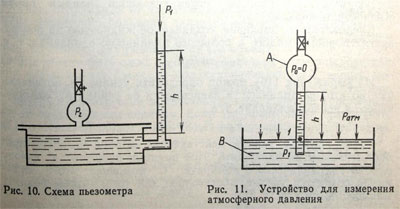
В этом случае давление на свободную поверхность столба жидкости равно нулю, так как весь воздух из сосуда А выкачан В то же время точка 1 находится на плоскости, проходящей через свободную поверхность. Следовательно, давление в этой точке равно атмосферному ратм.
Таким образом,
p0=yh или h=p0/y.
Следовательно, высота столба жидкости в соединительной трубке соответствует атмосферному давлению, действующему на свободную поверхность жидкости. Такой прибор называют барометром.
В некоторых случаях внешние силы, создающие давление в жидкости, настолько превосходят силы тяжести, что весом жидкости в расчетах можно пренебречь. В этом случае основное уравнение гидростатики (9) будет иметь вид
р=р0. (15)
Следовательно, при отсутствии сил тяжести давление во всех точках объема жидкости или газа одинаково.
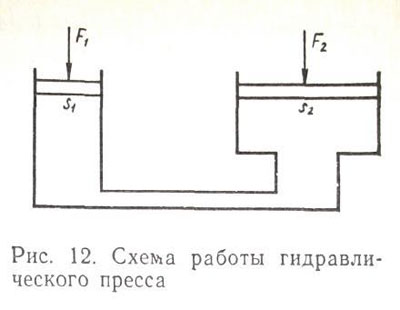
Этот принцип положен в основу работы гидравлического пресса, который состоит из двух сообщающихся сосудов (рис. 12), один из которых представляет собой малый цилиндр с поршнем площадью S1, а второй — большой цилиндр с поршнем площадью S2. Пусть на малый поршень действует сила F1. Определим, какую силу F2 надо приложить к поршню сечением S2, чтобы система находилась в равновесии. В соответствии с выражением (15) давление в жидкости в любой ее точке и на любую точку поверхности, ограничивающей данный объем жидкости, одинаково.
Следовательно, давление, создаваемое жидкостью на поверхностях поршней малого и большого цилиндров, одинаково, т. е.
F1/S1=F2/S2 . (16)
Из выражения (16) можно определить усилие F2, возникающее во втором цилиндре, в зависимости от усилия F1 действующего в первом цилиндре, т. е.
F2=F1 (S2/S1). (17)
Таким образом, усилия, действующие на поршни, прямо пропорциональны их площадям. Этот принцип положен в основу работы гидравлического домкрата. С помощью этого механизма создается усилие, достаточное для того, чтобы поднять машину, дом и т. п.
Сжимаемость. Известно, что молекулы капельной жидкости находятся достаточно близко одна от другой. Поэтому для их уплотнения необходимы большие сжимающие усилия. Сжимаемость капельной жидкости характеризуется коэффициентом объемного сжатия βw , который равен отношению относительного уменьшения объема жидкости ∆W/W к изменению избыточного давления ∆р:
βw=∆W/∆pW,
где W—первоначальный
объем жидкости; ∆W — изменение
объема при повышении давления на ∆р.
Например, для воды
изменение давления на ∆р = 105
Па приведет к снижению первоначального объема W на
1/20000, т. е.
∆W =(1/20 000) W.
Так как ∆W очень незначительна, то в расчетах обычно ею пренебрегают, считая воду и все капельные жидкости несжимаемыми.
Для газов при определении их сжимаемости используют другие зависимости.
Экспериментально доказано, что свойства газов и капельных жидкостей аналогичны.
Газы отличаются от капельных жидкостей тем, что при действии достаточно большого давления они могут быть сжаты до очень малого объема (во сколько раз увеличивается давление газа, во столько раз уменьшается его объем).
Газ может быть сжат до объема конечной величины, так как при значительной близости молекул начинают действовать молекулярные силы отталкивания, преодолеть которые трудно. С другой стороны, если предоставить газу большое пространство, то он займет его целиком. Если это пространство увеличить, то и возросший объем также будет равномерно заполнен газом, но давление газа в этом случае уменьшится.
Таким образом, объем и давление газа взаимосвязаны. Связь между давлением и объемом не однозначна, так как она зависит и от температуры. Чтобы понять, как эта связь осуществляется, будем исходить из того факта, что все вещества состоят из атомов.
Что такое
давление газа? Для ответа на этот
вопрос предположим, что газ находится в цилиндре, снабженном невесомым
подвижным поршнем (рис. 13).
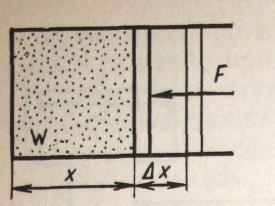
Рис 13.
Допустим, что вокруг цилиндра — вакуум. Так как внутри цилиндра атомы газа находятся в постоянном движении, то они постоянно, то они постоянно ударяются о стенки цилиндра (в том числе определения давления и о поршень). С каждым ударом молекул газа поршень постепенно перемещается вправо. Чтобы предотвратить такое перемещение, необходимо к поршню приложить усилие F. Если площадь поршня равна S, то действующая на него со стороны газа сила пропорциональна площади. В этом случае давление газа
p=F/S. (18)
Допустим, что количество молекул в заданном объеме цилиндра возросло. Это приведет к тому, что количество ударов молекул о поршень увеличится, поэтому необходимо увеличить силу, удерживающую поршень на месте. Следовательно, давление газа есть не что иное, как суммарное воздействие молекул, находящихся в замкнутом объеме.