Критерий балансируемости поршневых компрессоров высокого давления

В.А. Четвертаков

(Санкт-Петербургский государственный политехнический университет)

Статья была любезно предоставлена автором интернет-порталу www.remontcompressorov.ru для всеобщего обозрения. При копировании ссылка на первоисточник обязательна.

В течение последних десятилетий поршневые компрессоры все более интенсивно вытесняются из области низкого давления (до 2 МПа) винтовыми и другими ротационными машинами. В областях же среднего и высокого давлений (40 МПа и выше) продолжают доминировать поршневые компрессоры. По удельным показателям (масса, объем на единицу производительности) поршневые машины уступают ротационным. Поэтому одним из требований времени является повышение их быстроходности. Однако это невозможно без уравновешивания сил инерции механизма движения хотя бы на частоте вращения.

Наиболее быстроходные поршневые компрессоры выполняют по веерным и, реже, звездообразным схемам. При этом для уравновешивания противовесами на коленчатом вале каждая из этих схем требует обязательного соблюдения известных конструктивных условий. Это - специфические для каждой схемы углы между осями цилиндров, так называемые «углы развала» (V-90°, W-60°, VV-45° и др.), а также равенство масс поршневых групп по рядам либо их двукратное отношение для W-90° и VV-60°.

В конструкциях быстроходных ДВС или одноступенчатых компрессоров выполнение этих условий проблем не вызывает. При создании многоступенчатых поршневых машин соблюдение равенства масс поршней требует их искусственного утяжеления. Соблюдение равенства углов развала цилиндров вступает в противоречие с условием соседства цилиндровых гильз разного диаметра. Это вынуждает конструктора увеличивать радиальный габаритный размер машины и ее массу. Без потери качества уравновешивания нельзя произвольно раздвинуть ряды, чтобы разместить между ними, например, теплообменник или другой узел. Конечной целью этих конструктивных ограничений является круговая форма проекции годографа вектора суммарной поршневой силы Р_φ инерции первого порядка на поперечную плоскость машины. Собственно, такая форма годографа и делает возможным уравновешивание силы Р_φ противовесами на коленчатом вале.

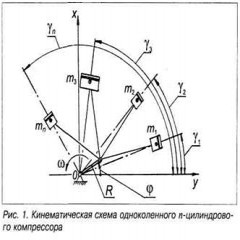
На рис. 1 изображена произвольная веерная схема многоступенчатого компрессора, а система уравнений, представляющая известный алгоритм расчета упомянутой проекции годографа силы Р_φ имеет вид:

С помощью этих тестовых выражений можно проверить на балансируемость любую одноколейную схему.

Между тем существует общий критерий балансируемости поршневых механизмов противовесами на валу [1, 2]. Он действителен для машин, в которых от одной поверхности последовательно приводятся в поступательное движение с периодом 2π/ω несколько поршней. Поверхность может быть вращающейся (колено вала, эксцентрик, наклонная к оси вала плоскость и др.) или прецессирующей (качающаяся шайба).

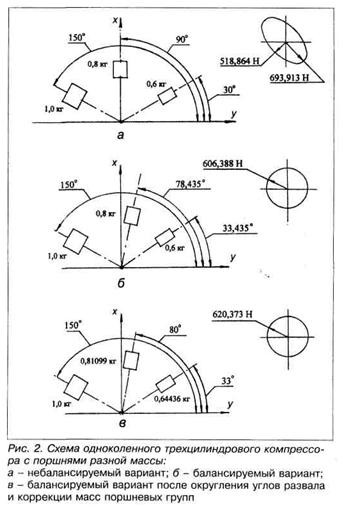
Действенность критерия подтверждается следующими примерами. На рис. 2, а и 3, а представлены две схемы с заведомым нарушением известных условий балансируемости - неравенством масс поршневых групп. Здесь и в последующих примерах приняты для определенности следующие численные значения: угловая скорость ω вала – 2 π16 с^-1, радиус R кривошипа -0,05 м, массы поршней - в кг. Расчет силы Р_φ по алгоритму (1) показывает, что в обоих случаях (рис. 2, а и 3, а) годограф Р_φ, как и следовало ожидать, имеет эллиптическую форму, т.е. уравновешивание Р_φ противовесами исключено.

Сохраняя неравенство масс поршневых групп, скорректируем углы γ₁ и γ₂ в варианте рис. 2, а, а также углы γ₃ и γ₄ в варианте рис. 3, а так, чтобы соблюдался критерий балансируемости. На рис. 2, б и 3, б приведены измененные схемы и результаты расчетов по тому же алгоритму (1). В обоих случаях модуль силы Р_φ стал постоянным, т.е. годографы получили форму круга. Как видим, сами по себе неравенство масс поршней и неравенство углов развала цилиндров не являются препятствием для балансировки механизма противовесами на валу.

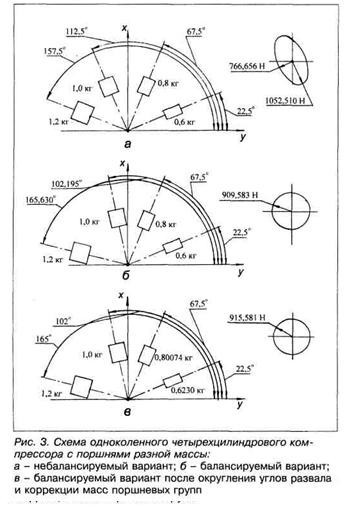
Поскольку практическое выполнение углов у_i, полученных при коррекции (33,435° и др.), технологически затруднительно, округлим их до простых значений, приведенных на рис. 2, е и 3, в. Если оставить массы поршней без изменения, округление углов вызовет некоторую деформацию годографов. Окружности вытянутся в эллипсы с соотношением осей соответственно 1,038 и 1,015. Однако, если даже столь малое нарушение балансируемости будет сочтено недопустимым, то критерий позволит коррекцией масс поршней восстановить балансируемость. На рис. 2, в и 3, в указаны эти откорректированные массы и результаты тестового расчета по алгоритму (1). Балансируемость после округления углов восстановилась, хотя модуль силы Р_φ в обоих случаях несколько вырос по сравнению с вариантами рис. 2, б и 3, б. Разумеется, для реальной балансировки компрессора столь высокая точность коррекции масс, как и постоянство модуля до шестого знака не требуются. Этот пример просто показывает, что углы развала можно произвольно изменить без ущерба для уравновешивания, если при этом скорректировать массы двух поршней.

Существование критерия балансируемости было обнаружено в ходе работы по снижению вибрации пятиступенчатого компрессора ЭКЗОА (40 МПа, 230 кВт, 980 об/мин) [3]. Компрессор был спроектирован в начале 60-х гг. на базе семицилиндрового звездообразного авиационного двигателя АИ-14, имевшего, естественно, одинаковые поршни и равные углы развала цилиндров. Поэтому нарушение известных условий балансируемости носило вынужденный характер. Компрессор имел цилиндры диаметром от 190 до 24 мм, поршневые группы массой от 3,63 до 5,44 кг, углы между осями цилиндров от 47,5° до 57,5°. Установка корректирующих масс 0,99 кг и 0,77 кг на юбки двух поршней позволила снизить суммарную силу инерции первого порядка на 33 дБ.

Формулировка критерия балансируемости следует из массово-геометрической интерпретации годографа вектора суммарной силы инерции первого порядка. Первые два равенства из системы (1) представим в виде

Можно заметить, что сомножители с символом суммирования являются моментами инерции некоторой жесткой плоской системы n точечных масс m_i, расположенных на осях цилиндров на удалении R от оси вращения вала (рис. 4):

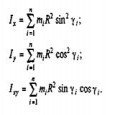
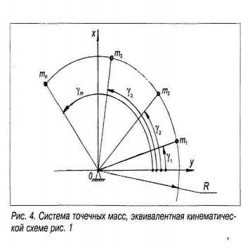
Тогда тестовый алгоритм (1) примет вид:

Из уравнений (3) следует, что при I_x=I_y и I_xy = 0

модуль силы Р_φ становится постоянным

проекция ее годографа на поперечную плоскость становится окружностью, а механизм движения компрессора получает возможность быть сбалансированным противовесами на коленчатом вале

Таким образом, может быть предложена следующая формулировка критерия балансируемости. Подлежащая проверке одноколейная веерная или звездообразная кинематическая схема представляется в виде эквивалентной плоской системы точечных масс, равных массам поршневых групп. Массы располагаются на осях цилиндров на равном удалении от оси вала. Условием балансируемости схемы является равенство осевых моментов инерции эквивалентной системы относительно любой пары ортогональных осей хОу, проходящих в ее плоскости через ось вала. Или, что то же самое, равенство нулю центробежного момента эквивалентной системы относительно любой такой пары осей, т.е.

I_x=I_y или I_xy = 0 (4)

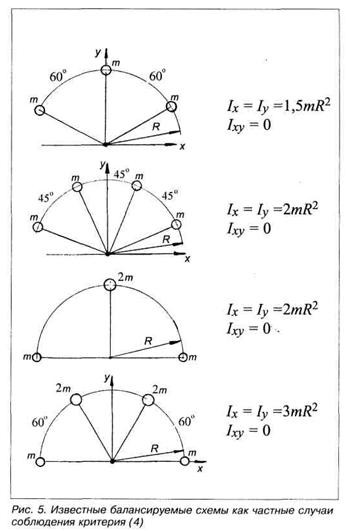
Можно удостовериться в том, что известные варианты балансируемых веерных схем являются лишь частными случаями соблюдения критерия (4), рис. 5.

О практическом использовании критерия. Теперь при проектировании высокооборотного многоступенчатого компрессора с одноколейным валом и числом цилиндров не менее трех необходимость подчинять конструкцию решению проблемы уравновешивания отпадает. Углы развала цилиндров и массы поршней следует выбирать, исходя из общих соображений минимизации массы и габаритных размеров, компактного размещения навесных узлов, эффективности охлаждения и т.п. После этого остается лишь рассчитать корректирующие массы для двух поршней. При этом можно выбрать такую пару поршней, у которых добавочные массы будут либо минимальны, либо наиболее просто образуемы конструктивно (утолщение юбки поршня, утяжеление крейцкопфного пальца и др.). Для определения размеров противовесов нет необходимости рассчитывать значение Р_φ по поверочному алгоритму (1). Меньшую часть S₁ статического момента противовесов, уравновешивающую вращающиеся массы, определяют общеизвестным путем. Большую же его часть S₂, уравновешивающую поршневые группы, следует определять как

где m _i, - массы поршневых групп с учетом корректирующих грузов и отнесенных к поступательному движению частей шатунов.

Убедиться в корректности выражения (5) можно, рассчитав центробежную силу этих частей противовесов Р_пр = S₂ ω² для любого из четырех балансируемых вариантов, т.е. для рис. 2, б, 2, в, 3, б или 3, в. Сравнение Р_пр и силы Р_φ для того же варианта обнаружит их полное равенство.

С помощью критерия можно обеспечить балансируемость также и двухцилиндрового V-образного компрессора, если по какой-либо причине нельзя выполнить угол развала равным 90°. В частности, это имеет место в компрессоре ЭК 10 (V- 60°, 3 м3/мин, 40 МПа) [3]. Для получения круговой формы годографа силы Р_φ здесь достаточно привести от колена вала уравновешивающий ползун нужной массы, размещенный в крышке картера. Такое решение является простой и малошумной альтернативой известному зубчатому механизму Ланчестера, использованному в ЭК10.

Вывод формул для расчета корректирующих масс приведен далее. Представим выражения для центробежных моментов эквивалентной системы масс по рис.4 как относительно пары осей хОу, так и относительно другой пары, x₁Оу₁, которая могла бы быть изображена на рис. 4 как результат поворота исходной пары на угол - 45°:

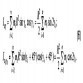
Для соблюдения условия (4) необходимо обеспечить равенство нулю обоих центробежных моментов. Выберем произвольно из i масс поршневых групп две массы, подлежащие коррекции, m_к и m_q, расположенные на углах γ_k и y_q. Условие (4) будет выполнено, если корректирующие массы Δm_к и Δm_q, добавленные соответственно к m_к и m_q, сведут к нулю оба центробежных момента, т.е.

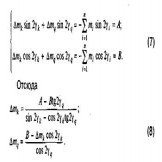
Необходимость решения обратной задачи - коррекции углов развала цилиндров при неизменных массах поршней по ступеням - представляется маловероятной. Однако и эта задача решается сведением к нулю центробежных моментов I_ху и I_x1y1 (6). Разница в том, что в левой части системы (7) оказываются полные массы m_к и m_q поршневых групп, осевые углы γ_k и y_q которых должны обеспечить балансируемость и являются предметом поиска. При этом правые части системы (7) включают в себя лишь данные остальных рядов схемы, не подлежащих смещению, т.е.

Решение системы уравнений (9):

где Ψ= arctg D/C, значения Ψ = 0...360⁰ в зависимости от знаков числителя и знаменателя;

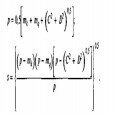
Побочным следствием соблюдения критерия балансируемости (4) является сведение к нулю наибольшего слагаемого инерционного реактивного момента на корпусе компрессорного агрегата. Для высокооборотного компрессора это может оказаться полезным.

В заключение надо отметить, что критерий (4) действителен также и для многоступенчатых компрессоров, выполненных по аксиально-поршневой схеме. Однако эта схема используется в компрессоростроении по ряду причин несравнимо реже кривошипной. Автору известны лишь многоступенчатые машины с качающейся шайбой ГКВ и КСВА в России и TGM в Германии. Поэтому излагать специфику применения критерия к этой схеме представляется пока нецелесообразным.

Список литературы

1. Четвертаков В.А. Об уравновешивании сил инерции
поршневых машин // Двигателестроение. 1991. №3.

2. Четвертаков В.А. Критерий уравновешивания сил инерции поршневых машин на частоте вращения // Компрессорная техника и пневматика. 1997. Вып. 1-2 (14-15).

3. Тигарев П.А. Справочник по судовым компрессорам. Л.: Судостроение, 1981.